本文作者简介:王夜笙,就读于郑州大学信息工程学院,感兴趣的方向为逆向工程和机器学习,长期从事数据抓取工作(长期与反爬虫技术作斗争~),
个人博客地址:http://bindog.github.
感谢怡轩同学的悉心指导~
之前拜读了靳志辉(@rickjin)老师写的《正态分布的前世今生》,一直对正态分布怀着一颗敬畏之心,刚好最近偶然看到python标准库中如何生成服从正态分布随机数的源码,觉得非常有趣,于是又去查找其他一些生成正态分布的方法,与大家分享一下。
利用中心极限定理生成正态分布
设$X_1,X_2,\cdots ,X_n$为独立同分布的随机变量序列,均值为$\mu$,方差为$\sigma^2$,则
$$Z_n=\frac{X_1+X_2+\cdots+X_n-n\mu}{\sigma \sqrt n}$$
具有渐近分布$N(0,1)$,也就是说当$n \rightarrow \infty$时,
$$P\left \{ \frac{X_1+X_2+\cdots+X_n-n\mu}{\sigma \sqrt n} \leq x \right \} \rightarrow \frac{1}{\sqrt{2\pi} } \int_{-\infty }^{x} e^{ -\frac{t^2}{2} } \, dt$$
换句话说,$n$个相互独立同分布的随机变量之和的分布近似于正态分布,$n$越大,近似程度越好。当然也有例外,比如$n$个独立同分布的服从柯西分布随机变量的算术平均数仍是柯西分布,这里就不扩展讲了。
根据中心极限定理,生成正态分布就非常简单粗暴了,直接生成n个独立同分布的均匀分布即可,看代码
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
def getNormal(SampleSize,n):
result = []
for i in range(SampleSize):
# 利用中心极限定理,[0,1)均匀分布期望为0.5,方差为1/12
iid = (np.mean(np.random.uniform(0,1,n))-0.5)*np.sqrt(12*n)
result.append(iid)
return result
# 生成10000个数,观察它们的分布情况
SampleSize = 10000
# 观察n选不同值时,对最终结果的影响
N = [1,2,10,1000]
plt.figure(figsize=(10,20))
subi = 220
for index,n in enumerate(N):
subi += 1
plt.subplot(subi)
normal = getNormal(SampleSize, n)
# 绘制直方图
plt.hist(normal,np.linspace(-4,4,81),facecolor="green",label="n={0}".format(n))
plt.ylim([0,450])
plt.legend()
plt.show()
得到结果如下图所示
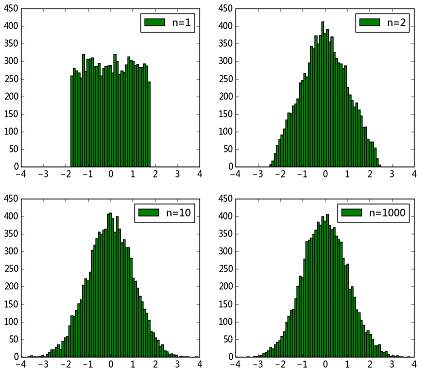
可以看到,$n=1$时其实就是均匀分布,随着$n$逐渐增大,直方图轮廓越来越接近正态分布了~因此利用中心极限定理暴力生成服从正态分布的随机数是可行的。但是这样生成正态分布速度是非常慢的,因为要生成若干个同分布随机变量,然后求和、计算,效率是非常低的。
利用逆变换法生成正态分布
假设$u=F(x)$是一个概率分布函数(CDF),$F^{-1}$是它的反函数,若$U$是一个服从$(0,1)$均匀分布的随机变量,则$F^{-1}(U)$服从函数$F$给出的分布。例如要生成一个服从指数分布的随机变量,我们知道指数分布的概率分布函数(CDF)为$F(x)=1 – e^{ – \lambda x}$,其反函数为$F^{-1}(x) = -\frac{\ln (1-x)}{\lambda}$,所以只要不断生成服从$(0,1)$均匀分布的随机变量,代入到反函数中即可生成指数分布。
正态分布的概率分布函数(CDF)如下图所示,
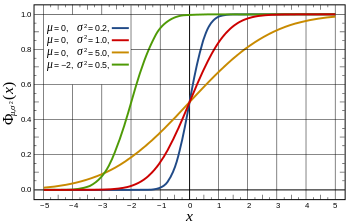
在y轴上产生服从(0,1)均匀分布的随机数,水平向右投影到曲线上,然后垂直向下投影到x轴,这样在x轴上就得到了正态分布。
当然正态分布的概率分布函数不方便直接用数学形式写出,求反函数也无从说起,不过好在scipy中有相应的函数,我们直接使用即可。
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
def getNormal(SampleSize):
iid = np.random.uniform(0,1,SampleSize)
result = norm.ppf(iid)
return result
SampleSize = 10000000
normal = getNormal(SampleSize)
plt.hist(normal,np.linspace(-4,4,81),facecolor="green")
plt.show()
结果如下图所示,
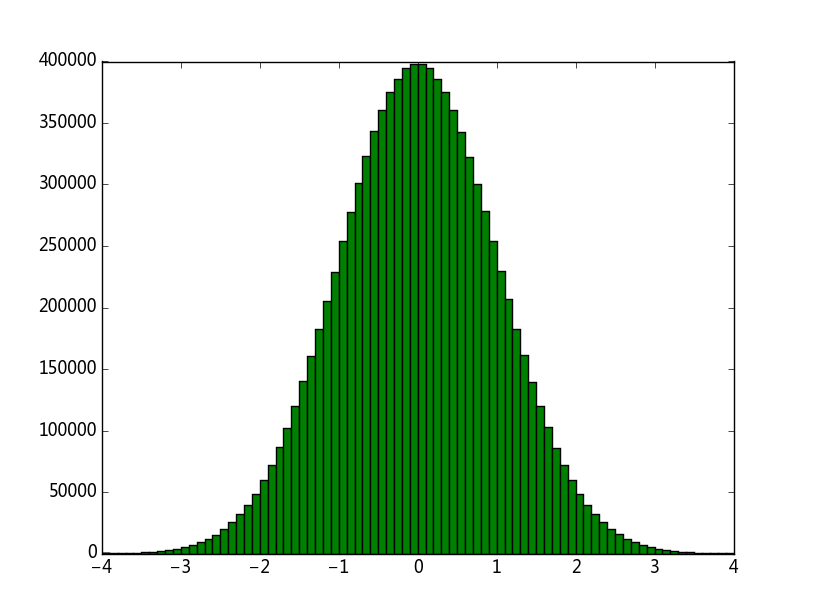
以上两个方法虽然方便也容易理解,但是效率实在太低,并不实用,那么在实际中到底是如何生成正态分布的呢?
Box–Muller算法
说来也巧,某天闲的无聊突然很好奇python是如何生成服从正态分布的随机数的,于是就看了看random.py的代码,具体实现的代码就不贴了,大家自己去看,注释中有下面几行
# When x and y are two variables from [0, 1), uniformly
# distributed, then
#
# cos(2*pi*x)*sqrt(-2*log(1-y))
# sin(2*pi*x)*sqrt(-2*log(1-y))
#
# are two *independent* variables with normal distribution
顿时感觉非常神奇,也就是说当$x$和$y$是两个独立且服从$(0,1)$均匀分布的随机变量时,$\cos (2\pi x) \cdot \sqrt { – 2\ln (1 – y)}$和$\sin (2\pi x) \cdot \sqrt { – 2\ln (1 – y)} $是两个独立且服从正态分布的随机变量!
后来查了查这个公式,发现这个方法叫做Box–Muller,其实本质上也是应用了逆变换法,证明方法比较多,这里我们选取一种比较好理解的
我们把逆变换法推广到二维的情况,设$U_1,U_2$为$(0,1)$上的均匀分布随机变量,$(U_1,U_2)$的联合概率密度函数为$f(u_1,u_2)=1(0 \le u_1,u_2 \le 1)$,若有:
$$\left\{\begin{matrix} {U_1} = {g_1}(X,Y)\\ {U_2} = {g_2}(X,Y) \end{matrix}\right.$$
其中,$g_1,g_2$的逆变换存在,记为
$$\left\{\begin{matrix} x = {h_1}({u_1},{u_2})\\ y = {h_2}({u_1},{u_2}) \end{matrix}\right.$$
且存在一阶偏导数,设$J$为Jacobian矩阵的行列式
$$ \left | J \right | =\begin{vmatrix} \frac{\partial x}{\partial u_1} & \frac{\partial x}{\partial u_2} \\ \frac{\partial y}{\partial u_1} & \frac{\partial y}{\partial u_2} \end{vmatrix} \ne 0$$
则随机变量$(X,Y)$的二维联合密度为(回顾直角坐标和极坐标变换):
$$f[h_1(u_1,u_2),h_2(u_1,u_2)] \cdot \left | J \right | = \left | J \right |$$
根据这个定理我们来证明一下,
$$\left\{\begin{matrix} Y_1 = \sqrt {- 2\ln X_1} \cos (2\pi X_2) \\ Y_2 = \sqrt {- 2\ln X_1} \sin (2\pi X_2) \end{matrix}\right.$$
求反函数得
$$\left\{\begin{matrix} X_1 = e^{ – \frac{Y_1^2 + Y_2^2}{2}} \\ X_2 = \frac{1}{2 \pi} \arctan \frac{Y_2}{Y_1} \end{matrix}\right.$$
计算Jacobian行列式
$$\begin{align} \left | J \right | =\begin{vmatrix} \frac{\partial X_1}{\partial Y_1} & \frac{\partial X_1}{\partial Y_2} \\ \frac{\partial X_2}{\partial Y_1} & \frac{\partial X_2}{\partial Y_2} \end{vmatrix} & = \begin{vmatrix} -Y_1 \cdot e^{ -\frac{1}{2}(Y_1^2 + Y_2^2)} & -Y_2 \cdot e^{-\frac{1}{2}(Y_1^2 + Y_2^2)} \\ -\frac{Y_2}{2 \pi (Y_1^2+Y_2^2)} & \frac{Y_1}{2 \pi (Y_1^2+Y_2^2)} \end{vmatrix} \\ & =e^{-\frac{1}{2}(Y_1^2 + Y_2^2)}[\frac{-Y_1^2}{2 \pi (Y_1^2 + Y_2^2)}-\frac{Y_2^2}{2 \pi (Y_1^2 + Y_2^2)}] \\ & =-\frac{1}{2 \pi}e^{-\frac{1}{2}(Y_1^2 + Y_2^2)} \\ & =-(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}Y_1^2})(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}Y_2^2}) \end{align}$$
由于$X_1,X_2$为$(0,1)$上的均匀分布,概率密度函数均为$1$,所以$Y_1,Y_2$的联合概率密度函数为$-(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}Y_1^2})(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}Y_2^2})$,熟悉二维正态分布的就知道是两个独立的正态分布,所以$Y_1,Y_2$是两个独立且服从正态分布的随机变量~
写程序实现一下
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
def getNormal(SampleSize):
iid = np.random.uniform(0,1,SampleSize)
normal1 = np.cos(2*np.pi*iid[0:SampleSize/2-1])*np.sqrt(-2*np.log(iid[SampleSize/2:SampleSize-1]))
normal2 = np.sin(2*np.pi*iid[0:SampleSize/2-1])*np.sqrt(-2*np.log(iid[SampleSize/2:SampleSize-1]))
return np.hstack((normal1,normal2))
# 生成10000000个数,观察它们的分布情况
SampleSize = 10000000
normal = getNormal(SampleSize)
plt.hist(normal,np.linspace(-4,4,81),facecolor="green")
plt.show()
得到的结果如下图所示,
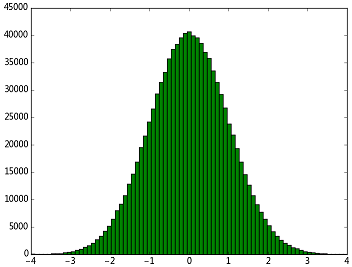
这里抽样次数达到1千万次,1秒左右就完成了,速度非常快~
Ziggurat算法
Box–Muller算法虽然非常快,但是由于用到了三角函数和对数函数,相对来说还是比较耗时的,如果想要更快一点有没有办法呢?
当然有,这就是Ziggurat算法,不仅可以用于快速生成正态分布,还可以生成指数分布等等。Ziggurat算法的基本思想是利用拒绝采样,什么是拒绝采样呢?
拒绝采样(Rejection Sampling),有的时候也称接收-拒绝采样,使用场景是有些函数$p(x)$太复杂在程序中没法直接采样,那么可以设定一个程序可抽样的分布$q(x)$比如正态分布等等,然后按照一定的方法拒绝某些样本,达到接近$p(x)$分布的目的:
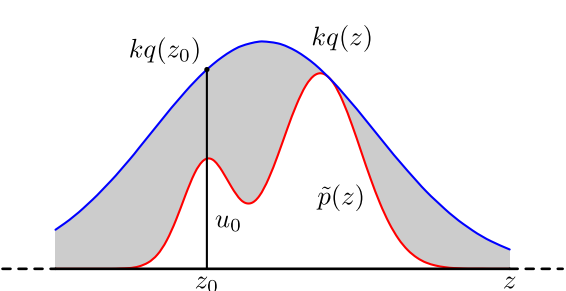
具体操作如下,设定一个方便抽样的函数$q(x)$,以及一个常量$k$,使得$p(x)$总在$kq(x)$的下方。(参考上图)
$x$轴方向:从$q(x)$分布抽样得到$a$$y$轴方向:从均匀分布$(0, kq(a))$中抽样得到$u$- 如果刚好落到灰色区域:
$u>p(a)$,拒绝;否则接受这次抽样 - 重复以上过程
证明过程就不细说了,知道怎么用就行了,感兴趣的可以看看这个文档
不过在高维的情况下,拒绝采样会出现两个问题,第一是合适的$q$分布比较难以找到,第二是很难确定一个合理的$k$值。这两个问题会造成图中灰色区域的面积变大,从而导致拒绝率很高,无用计算增加。
采用拒绝采样来生成正态分布,最简单直观的方法莫过于用均匀分布作为$q(x)$,但是这样的话,矩形与正态分布曲线间的距离很大,就会出现刚才提到的问题,高效也就无从谈起了。
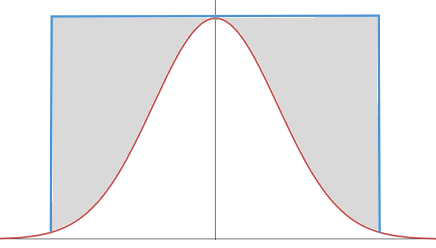
而Ziggurat算法高效的秘密在于构造了一个非常精妙的$q(x)$,看下面这张图
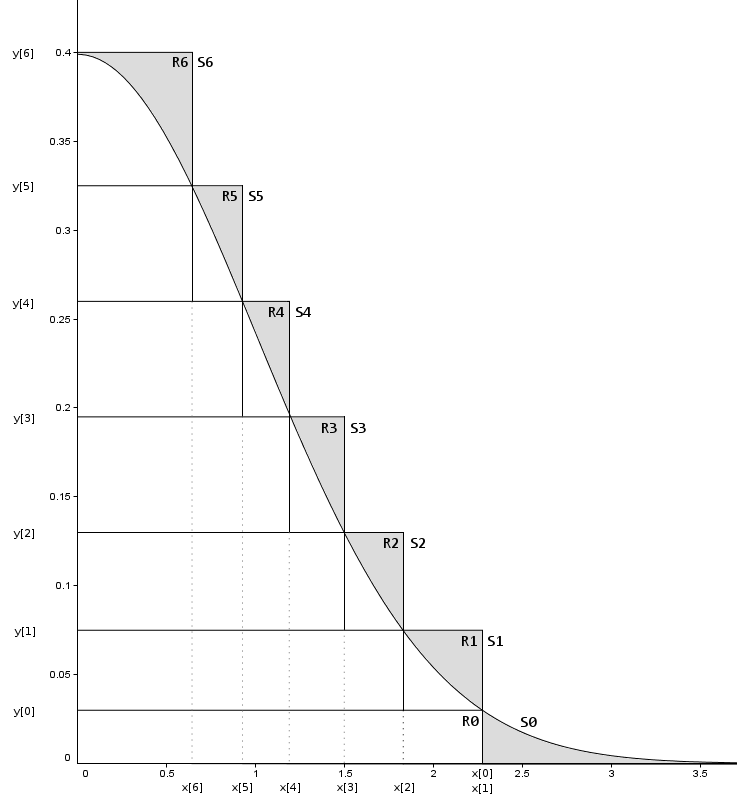
我们用多个堆叠在一起的矩形,这样保证阴影部分(被拒绝部分)的始终较小,这样就非常高效了
简单对图作一个解释:
- 我们用
R[i]来表示一个矩形,R[i]的右边界为x[i],上边界为y[i]。S[i]表示一个分割,当i=0时,S[0]=R[0]+tail,其他情况S[i]==R[i] - 除了
R[0]以外,其他每个矩形面积相等,设为定值A。R[0]的面积=A-tail的面积。这样保证从任何一个分割中抽样(x,y)的概率相等 - 当任意选定一个
R[i]在其中抽样(x,y),若x<x[i+1],y必然在曲线下方,满足条件,接受x;若x[i+1]<x<x[i],则还需要进一步判断。同样这里R[0]和tail中的样本需要进行特殊处理 - 这里为了方便解释,只用了几个矩形,在程序实现的时候,一般使用
128或256个矩形
可以看出,为了提高效率,Ziggurat算法中使用了许多技巧性的东西,这在其C代码实现中更加明显,使用了与运算和字节等各种小技巧,代码就不在这里贴了,感兴趣可以看看下面几个版本,C版本的追求的是极致的速度,每个矩形的边界已经提前计算好了。C#版本中的注释非常详细,Java版的基本与C#一致,但是效率一般。
最后对比一下Ziggurat算法与Box-muller算法的效率
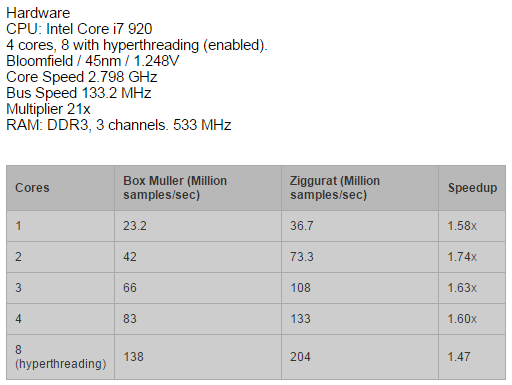
总结
本文介绍了多种生成正态分布的方法,其中Box-muller算法应对一般的需求足够了,但是要生成大量服从正态分布的随机数时,Ziggurat算法效率会更高一点~
再说点题外话,作为一名普通的程序员,对于很多东西往往不需要了解的非常深入,说白了“会用就行了”。但是有的时候探寻其背后的原理往往能发现别人领会不到的数学之美,这也是写程序之余的一点乐趣吧~

发表/查看评论