书接前文。跟 ROC 类似,Lift(提升)和 Gain(增益)也一样能简单地从以前的 Confusion Matrix 以及 Sensitivity、Specificity 等信息中推导而来,也有跟一个 baseline model 的比较,然后也是很容易画出来,很容易解释。以下先修知识,包括所需的数据集:
一些准备
说,混淆矩阵 (Confusion Matrix) 是我们永远值得信赖的朋友:
| 预测 | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| 实 | 1 | d, True Positive | c, False Negative | c+d, Actual Positive |
| 际 | 0 | b, False Positive | a, True Negative | a+b, Actual Negative |
| b+d, Predicted Positive | a+c, Predicted Negative |
几个术语需要随时记起:
- Sensitivity(覆盖率,True Positive Rate)= 正确预测到的正例数 / 实际正例总数 Recall (True Positive Rate,or Sensitivity) =true positive/total actual positive=d/c+d
- PV+ (命中率,Precision, Positive Predicted Value) = 正确预测到的正例数 / 预测正例总数 Precision (Positive Predicted Value, PV+) =true positive/ total predicted positive=d/b+d
- Specificity (负例的覆盖率,True Negative Rate) = 正确预测到的负例个数 / 实际负例总数 Specificity (True Negative Rate) =true negative/total actual negative=a/a+b
首先记我们 valid 数据中,正例的比例为 pi1(念做 pai 1),在我们的例子中,它等于 c+d/a+b+c+d=0.365。单独提出 pi1,是因为有时考虑 oversampling 后的一些小调整,比如正例的比例只有 0.001,但我们把它调整为 0.365(此时要在 SAS proc logistic 回归的 score 语句加一个 priorevent=0.001 选项)。本文不涉及 oversampling。现在定义些新变量:
Ptp=proportion of true positives=d/a+b+c+d=(c+d/a+b+c+d)*(d/c+d) =pi1* Sensitivity,正确预测到的正例个数占总观测值的比例
Pfp=proportion of false positives=b/a+b+c+d= (a+b/a+b+c+d)*(b/a+b) = (1-c+d/a+b+c+d)*(1-a/a+b) = (1-pi1)*(1- Specificity) ,把负例错误地预测成正例的个数占总数的比例
Depth=proportion allocated to class 1=b+d/a+b+c+d=Ptp+Pfp,预测成正例的比例
PV_plus=Precision (Positive Predicted Value, PV+) = d/b+d=Ptp/depth,正确预测到的正例数占预测正例总数的比例
Lift= (d/b+d)/(c+d/a+b+c+d)=PV_plus/pi1,提升值,解释见下节。
以上都可以利用 valid_roc 数据计算出来:
%let pi1=0.365;
data valid_lift;
set valid_roc;
cutoff=PROB;
Ptp=&pi1*SENSIT;
Pfp=(1-&pi1)*1MSPEC;
depth=Ptp+Pfp;
PV_plus=Ptp/depth;
lift=PV_plus/&pi1;
keep cutoff SENSIT 1MSPEC depth PV_plus lift;
run;
先前我们说 ROC curve 是不同阈值下 Sensitivity 和 1-Specificity 的轨迹,类似,
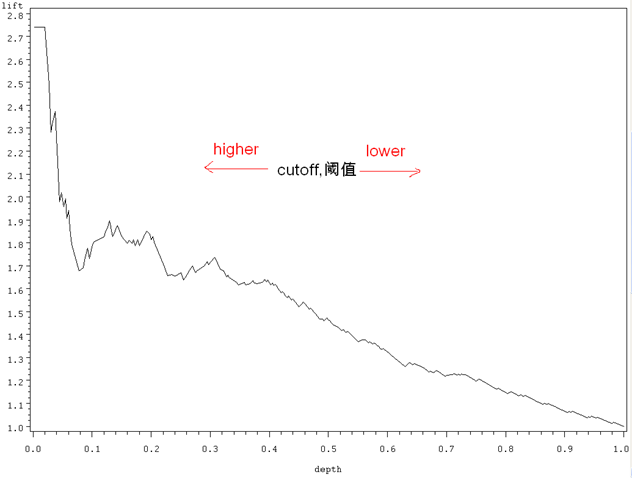
Lift chart 是不同阈值下 Lift 和 Depth 的轨迹
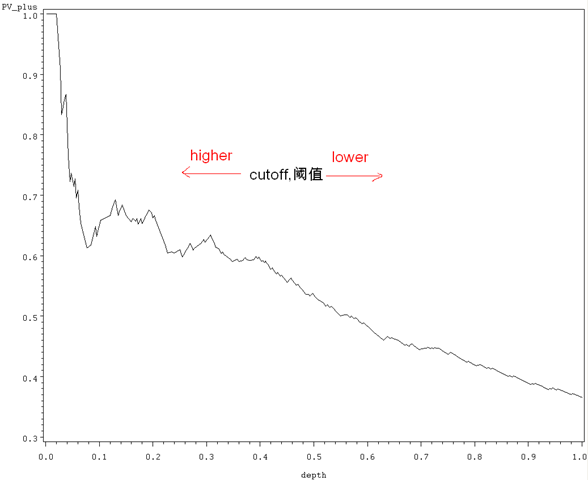
Gains chart 是不同阈值下 PV + 和 Depth 的轨迹
Lift
Lift = (d/b+d)/(c+d/a+b+c+d)=PV_plus/pi1),这个指标需要多说两句。它衡量的是,与不利用模型相比,模型的预测能力 “变好” 了多少。不利用模型,我们只能利用 “正例的比例是 c+d/a+b+c+d” 这个样本信息来估计正例的比例(baseline model),而利用模型之后,我们不需要从整个样本中来挑选正例,只需要从我们预测为正例的那个样本的子集(b+d)中挑选正例,这时预测的准确率为 d/b+d。
显然,lift(提升指数)越大,模型的运行效果越好。如果这个模型的预测能力跟 baseline model 一样,那么 d/b+d 就等于 c+d/a+b+c+d(lift 等于 1),这个模型就没有任何 “提升” 了(套一句金融市场的话,它的业绩没有跑过市场)。这个概念在数据库营销中非常有用,举个例子:
比如说你要向选定的 1000 人邮寄调查问卷(a+b+c+d=1000)。以往的经验告诉你大概 20% 的人会把填好的问卷寄回给你,即 1000 人中有 200 人会对你的问卷作出回应(response,c+d=200),用统计学的术语,我们说 baseline response rate 是 20%(c+d/a+b+c+d=20%)。
如果你现在就漫天邮寄问卷,1000 份你期望能收回 200 份,这可能达不到一次问卷调查所要求的回收率,比如说工作手册规定邮寄问卷回收率要在 25% 以上。
通过以前的问卷调查,你收集了关于问卷采访对象的相关资料,比如说年龄、教育程度之类。利用这些数据,你确定了哪类被访问者对问卷反应积极。假设你已经利用这些过去的数据建立了模型,这个模型把这 1000 人分了类,现在你可以从你的千人名单中挑选出反应最积极的 100 人来(b+d=100),这 10% 的人的反应率 (response rate)为 60%(d/b+d=60%,d=60)。那么,对这 100 人的群体(我们称之为 Top 10%),通过运用我们的模型,相对的提升 (lift value) 就为 60%/20%=3;换句话说,与不运用模型而随机选择相比,运用模型而挑选,效果提升了 3 倍。
上面说 lift chart 是不同阈值下 Lift 和 Depth 的轨迹,先画出来:
symbol i=join v=none c=black;
proc gplot data=valid_lift;
plot lift*depth;
run; quit;
上图的纵坐标是 lift,意义已经很清楚。横坐标 depth 需要多提一句。以前说过,随着阈值的减小,更多的客户就会被归为正例,也就是 depth(预测成正例的比例)变大。当阈值设得够大,只有一小部分观测值会归为正例,但这一小部分(一小撮)一定是最具有正例特征的观测值集合(用上面数据库营销的例子来说,这一部分人群对邮寄问卷反应最为活跃),所以在这个 depth 下,对应的 lift 值最大。
同样,当阈值设定得足够的小,那么几乎所有的观测值都会被归为正例(depth 几乎为 1)——这时分类的效果就跟 baseline model 差不多了,相对应的 lift 值就接近于 1。
一个好的分类模型,就是要偏离 baseline model 足够远。在 lift 图中,表现就是,在 depth 为 1 之前,lift 一直保持较高的(大于 1 的)数值,也即曲线足够的陡峭。
注:在一些应用中(比如信用评分),会根据分类模型的结果,把样本分成 10 个数目相同的子集,每一个子集称为一个 decile,其中第一个 decile 拥有最多的正例特征,第二个 decile 次之,依次类推,以上 lift 和 depth 组合就可以改写成 lift 和 decile 的组合,也称作 lift 图,含义一样。刚才提到,“随着阈值的减小,更多的客户就会被归为正例,也就是 depth(预测成正例的比例)变大。当阈值设得够大,只有一小部分观测值会归为正例,但这一小部分(第一个 decile)一定是最具有正例特征的观测值集合。”
Gains
Gains (增益) 与 Lift (提升)相当类似:Lift chart 是不同阈值下 Lift 和 Depth 的轨迹,Gains chart 是不同阈值下 PV + 和 Depth 的轨迹,而 PV+=lift*pi1= d/b+d(见上),所以它们显而易见的区别就在于纵轴刻度的不同:
symbol i=join v=none c=black;
proc gplot data=valid_lift;
plot pv_plus*depth;
run; quit;
上图阈值的变化,含义与 lift 图一样。随着阈值的减小,更多的客户就会被归为正例,也就是 depth(预测成正例的比例,b+d/a+b+c+d)变大(b+d 变大),这样 PV+(d/b+d,正确预测到的正例数占预测正例总数的比例)就相应减小。当阈值设定得足够的小,那么几乎所有的观测值都会被归为正例(depth 几乎为 1),那么 PV + 就等于数据中正例的比例 pi1 了(这里是 0.365。在 Lift 那一节里,我们说此时分类的效果就跟 baseline model 差不多,相对应的 lift 值就接近于 1,而 PV+=lift*pi1。Lift 的 baseline model 是纵轴上恒等于 1 的水平线,而 Gains 的 baseline model 是纵轴上恒等于 pi1 的水平线)。显然,跟 lift 图类似,一个好的分类模型,在阈值变大时,相应的 PV + 就要变大,曲线足够陡峭。
注:我们一般看到的 Gains Chart,图形是往上走的,咋一看跟上文相反,其实道理一致,只是坐标选择有差别,不提。
总结和下期预告:K-S
以上提到的 ROC、Lift、Gains,都是基于混淆矩阵及其派生出来的几个指标(Sensitivity 和 Specificity 等等)。如果愿意,你随意组合几个指标,展示到二维空间,就是一种跟 ROC 平行的评估图。比如,你 plot Sensitivity*Depth 一把,就出一个新图了,——很不幸,这个图叫做 Lorentz Curve(劳伦兹曲线),不过你还可以尝试一下别的组合,然后凑一个合理的解释。
Gains chart 是不同阈值下 PV + 和 Depth 的轨迹(Lift 与之类似),而 ROC 是 sensitivity 和 1-Specificity 的对应,前面还提到,Sensitivity(覆盖率,True Positive Rate)在欺诈监控方面更有用(所以 ROC 更适合出现在这个场合),而 PV + 在数据库营销里面更有用(这里多用 Gains/Lift)。
混淆矩阵告一段落。接下来将是 K-S(Kolmogorov-Smirnov)。参考资料同上一篇。

发表 / 查看评论