1. 神奇的Gamma函数
1.1 Gamma 函数诞生记
学高等数学的时候,我们都学习过如下一个长相有点奇特的Gamma函数
$$ \Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}dt $$
通过分部积分的方法,可以推导出这个函数有如下的递归性质
$$\Gamma(x+1) = x \Gamma(x)$$
于是很容易证明,\(\Gamma(x)\)函数可以当成是阶乘在实数集上的延拓,具有如下性质
$$\Gamma(n) = (n-1)! $$
学习了Gamma函数之后,多年以来我一直有两个疑问:
- 这个长得这么怪异的一个函数,数学家是如何找到的;
- 为何定义
\(\Gamma\)函数的时候,不使得这个函数的定义满足\(\Gamma(n) = n!\)而是\(\Gamma(n) = (n-1)! \)
最近翻了一些资料,发现有不少文献资料介绍Gamma函数发现的历史,要说清楚它需要一定的数学推导,这儿只是简要的说一些主线。
1728年,哥德巴赫在考虑数列插值的问题,通俗的说就是把数列的通项公式定义从整数集合延拓到实数集合,例如数列\(1,4,9,16,\cdots\)可以用通项公式\(n^2\)自然的表达,即便\(n\)为实数的时候,这个通项公式也是良好定义的。直观的说也就是可以找到一条平滑的曲线\(y=x^2\)通过所有的整数点\((n,n^2)\),从而可以把定义在整数集上的公式延拓到实数集合。一天哥德巴赫开始处理阶乘序列\(1,2,6,24,120,720,\cdots\),我们可以计算\(2!,3!\),是否可以计算\(2.5!\)呢?我们把最初的一些\((n,n!)\)的点画在坐标轴上,确实可以看到,容易画出一条通过这些点的平滑曲线。

但是哥德巴赫无法解决阶乘往实数集上延拓的这个问题,于是写信请教尼古拉斯.贝努利和他的弟弟丹尼尔.贝努利,由于欧拉当时和丹尼尔.贝努利在一块,他也因此得知了这个问题。而欧拉于1729 年完美的解决了这个问题,由此导致了\(\Gamma\)函数的诞生,当时欧拉只有22岁。
事实上首先解决\(n!\)的插值计算问题的是丹尼尔.贝努利,他发现,
如果\(m,n\)都是正整数,如果\(m \rightarrow \infty\),有
$$ \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m-1+n)}(m+\frac{n}{2})^{n-1} \rightarrow n! $$
于是用这个无穷乘积的方式可以把\(n!\)的定义延拓到实数集合。例如,取\(n=2.5\),\(m\)足够大,基于上式就可以近似计算出\(2.5!\)。
欧拉也偶然的发现\(n!\)可以用如下的一个无穷乘积表达
\begin{equation} \label{euler-series} \Bigl[\Bigl(\frac{2}{1}\Bigr)^n\frac{1}{n+1}\Bigr] \Bigl[\Bigl(\frac{3}{2}\Bigr)^n\frac{2}{n+2}\Bigr] \Bigl[\Bigl(\frac{4}{3}\Bigr)^n\frac{3}{n+3}\Bigr] \cdots = n! \quad (*) \end{equation}
用极限形式,这个式子整理后可以写为
\begin{equation} \label{euler-series2} \lim_{m \rightarrow \infty} \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m+n)}(m+1)^{n} = n! \quad (**) \end{equation}
左边可以整理为
\begin{align*} & \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m+n)}(m+1)^{n} \\ = & 1\cdot 2\cdot 3 \cdots n \cdot \frac{(n+1)(n+2)\cdots m}{(1+n)(2+n)\cdots m } \cdot \frac{(m+1)^{n}}{(m+1)(m+2)\cdots (m+n)} \\ = & n! \frac{(m+1)^{n}}{(m+1)(m+2)\cdots (m+n)} \\ = & n!\prod_{k=1}^{n} \frac{m+1}{m+k} \rightarrow n! \qquad (m\rightarrow \infty) \end{align*}
所以 (*)、(**)式都成立。
欧拉开始尝试从一些简单的例子开始做一些计算,看看是否有规律可循,欧拉极其擅长数学的观察与归纳。当\(n=1/2\)的时候,带入(*)式计算,整理后可以得到
$$\Bigl(\frac{1}{2}\Bigr)! = \sqrt{\frac{2\cdot4}{3\cdot3} \cdot \frac{4\cdot6}{5\cdot5}\cdot \frac{6\cdot8}{7\cdot7} \cdot \frac{8\cdot10}{9\cdot9} \cdots}$$
然而右边正好和著名的 Wallis 公式关联。Wallis 在1665年使用插值方法计算半圆曲线\(y = \sqrt{x(1-x)}\)下的面积(也就是直径为1的半圆面积)的时候,得到关于\(\pi\)的如下结果,
$$ \frac{2\cdot4}{3\cdot3} \cdot \frac{4\cdot6}{5\cdot5}\cdot \frac{6\cdot8}{7\cdot7} \cdot \frac{8\cdot10}{9\cdot9} \cdots = \frac{\pi}{4}$$
于是,欧拉利用 Wallis 公式得到了如下一个很漂亮的结果
$$ \Bigl(\frac{1}{2}\Bigr)! = \frac{\sqrt{\pi}}{2} $$

大数学家欧拉
欧拉和高斯都是具有超凡直觉的数学家,但是欧拉和高斯的风格迥异。高斯是个老狐狸,数学上非常严谨,发表结果的时候却都把思考的痕迹抹去,只留下漂亮的结果,这招致了一些数学家对高斯的批评;而欧拉的风格不同,经常通过经验直觉做大胆的猜测,而他的文章中往往留下他如何做数学猜想的痕迹,而文章有的时候论证不够严谨。 拉普拉斯曾说过:”读读欧拉,他是所有人的老师。”波利亚在他的名著《数学与猜想》中也对欧拉做数学归纳和猜想的方式推崇备至。
欧拉看到\((\frac{1}{2})!\)中居然有\(\pi\),对数学家而言,有\(\pi\)的地方必然有和圆相关的积分。由此欧拉猜测\(n!\)一定可以表达为某种积分形式,于是欧拉开始尝试把\(n!\)表达为积分形式。虽然Wallis的时代微积分还没有发明出来,Wallis是使用插值的方式做推导计算的,但是Wallis公式的推导过程基本上就是在处理积分\(\int_0^1x^\frac{1}{2}(1-x)^\frac{1}{2}dx\),受Wallis的启发,欧拉开始考虑如下的一般形式的积分
$$ J(e,n) = \int_0^1 x^e(1-x)^ndx$$
此处n 为正整数,\(e\)为正实数。利用分部积分方法,容易得到
$$ J(e,n) = \frac{n}{e+1}J(e+1,n-1) $$
重复使用上述迭代公式,最终可以得到
$$ J(e,n) = \frac{1\cdot2\cdots n}{(e+1)(e+2)\cdots(e+n+1)} $$
于是欧拉得到如下一个重要的式子
$$ n! = (e+1)(e+2)\cdots(e+n+1)\int_0^1 x^e(1-x)^ndx $$
接下来,欧拉使用了一点计算技巧,取\(e=f/g\)并且令\(f \rightarrow 1, g \rightarrow 0\),
然后对上式右边计算极限(极限计算的过程此处略去,推导不难,有兴趣的同学看后面的参考文献吧),于是欧拉得到如下简洁漂亮的结果:
$$ n! = \int_0^1 (-\log t)^ndt $$
欧拉成功的把\(n!\)表达为了积分形式!如果我们做一个变换\(t=e^{-u}\),就可以得到我们常见的Gamma函数形式
$$ n! = \int_0^{\infty} u^ne^{-u}du $$
于是,利用上式把阶乘延拓到实数集上,我们就得到Gamma函数的一般形式
$$ \Gamma(x) = \int_0^1 (-\log t)^{x-1}dt = \int_0^{\infty} t^{x-1}e^{-t}dt $$
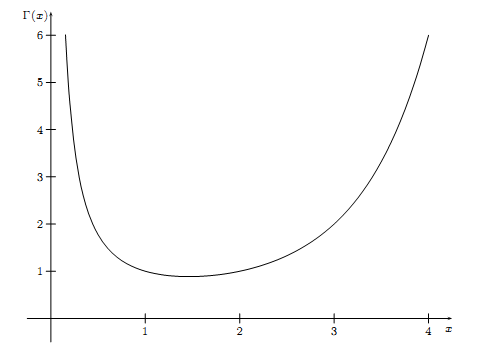
Gamma函数找到了,我们来看看第二个问题,为何Gamma函数被定义为\(\Gamma(n)=(n-1)!\),这看起来挺别扭的。如果我们稍微修正一下,把Gamma函数定义中的\(t^{x-1}\)替换为\(t^x\)
$$ \Gamma(x) = \int_0^{\infty} t^{x}e^{-t}dt $$
这不就可以使得\(\Gamma(n)=n!\)了嘛。欧拉最早的Gamma函数定义还真是如上所示,选择了\(\Gamma(n)=n!\),可是欧拉不知出于什么原因,后续修改了Gamma函数的定义,使得\(\Gamma(n)=(n-1)!\)。而随后勒让德等数学家对Gamma函数的进一步深入研究中,认可了这个定义,于是这个定义就成为了既成事实。有数学家猜测,一个可能的原因是欧拉研究了如下积分
$$ B(m, n) = \int_0^1 x^{m-1}(1-x)^{n-1}dx $$
这个函数现在称为Beta函数。如果Gamma函数的定义选取满足\(\Gamma(n)=(n-1)!\),那么有
$$ B(m,n) = \frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)} $$
非常漂亮的对称形式。可是如果选取\(\Gamma(n)=n!\)的定义,令
$$ E(m, n) = \int_0^1 x^{m}(1-x)^{n}dx $$
则有
$$ E(m,n) = \frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n+1)} $$
这个形式显然不如\(B(m,n)\)优美,而数学家总是很在乎数学公式的美感的。
要了解更多的Gamma函数的历史,推荐阅读
- Philip J. Davis,Leonhard Euler’s Integral: A Historical Profile of the Gamma Function
- Jacques Dutka,The Early History of the Factorial Function
- Detlef Gronnau,Why is the gamma function so as it is?
1.2 Gamma函数欣赏
Each generation has found something of interest to say about the gamma function. Perhaps the next generation will also.
– Philip J.Davis
Gamma函数从它诞生开始就被许多数学家进行研究,包括高斯、勒让德、威尔斯特拉斯、柳维尔等等。这个函数在现代数学分析中被深入研究,在概率论中也是无处不在,很多统计分布都和这个函数相关。Gamma函数作为阶乘的推广,首先它也有和Stirling公式类似的一个结论
$$ \Gamma(x) \sim \sqrt{2\pi}e^{-x}x^{x-\frac{1}{2}}$$
另外,Gamma函数不仅可以定义在实数集上,还可以延拓到整个复平面上。
复平面上的Gamma函数
Gamma函数有很多妙用,它不但使得(1/2)!的计算有意义,还能扩展很多其他的数学概念。比如导数,我们原来只能定义一阶、二阶等整数阶导数,有了Gamma函数我们可以把函数导数的定义延拓到实数集,从而可以计算1/2阶导数,同样的积分作为导数的逆运算也可以有分数阶。我们先考虑一下\(x^n\)的各阶导数
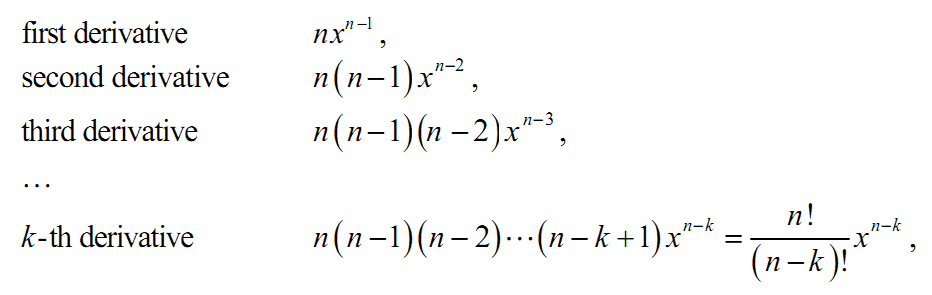
由于k阶导数可以用阶乘表达,于是我们用Gamma函数表达为
$$ \frac{\Gamma{(n+1)}}{\Gamma{(n-k+1)}} x^{n-k} $$
于是基于上式,我们可以把导数的阶从整数延拓到实数集。例如,取\(n=1, k=\frac{1}{2}\)我们可以计算\(x\)的\(\frac{1}{2}\)阶导数为
$$ \frac{\Gamma{(1+1)}}{\Gamma{(1-1/2+1)}} x^{1-1/2} = \frac{2\sqrt{x}}{\sqrt{\pi}}$$
很容易想到对于一般的函数\(f(x)\)通过Taylor级数展开可以表达为幂级数,于是借用\(x^n\)的分数阶导数,我们可以尝试定义出任意函数的分数阶导数。不过有点遗憾的是这种定义方法并非良定义的,不是对所有函数都适用,但是这个思想却是被数学家广泛采纳了,并由此发展了数学分析中的一个研究课题:Fractional Calculus,在这种微积分中,分数阶的导数和积分都具有良定义,而这都依赖于Gamma函数。
Gamma函数和欧拉常数\(\gamma\)有密切关系,可以发现
$$ \gamma = -\frac{d\Gamma(x)}{dx}|_{x=1} =\lim_{n\rightarrow \infty}(1+\frac{1}{2} + \frac{1}{3}+\cdots+\frac{1}{n} - \log n)$$
进一步还可以发现 Gamma 函数和黎曼函数\(\zeta(s)\)有密切联系,
$$ \zeta(s) = 1+\frac{1}{2^s} + \frac{1}{3^s} + \cdots $$
而\(\zeta\) 函数涉及了数学中著名的黎曼猜想和素数的分布定理。希尔伯特曾说,如果他在沉睡1000年后醒来,他将问的第一个问题便是:黎曼猜想得到证明了吗?
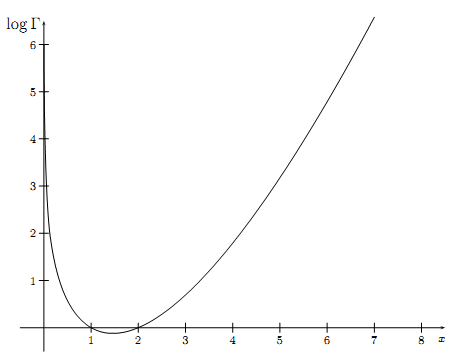
\(\log \Gamma(x)\)
从Gamma函数的图像我们可以看到它是一个凸函数,不仅如此,\(\log\Gamma(x)\)也是一个凸函数,数学上可以证明如下定理:
[Bohr-Mullerup定理] 如果\(f:(0,\infty)\rightarrow(0,\infty)\),且满足
\(f(1) = 1\)\(f(x+1) = xf(x)\)\(\log f(x)\)是凸函数
那么\(f(x) = \Gamma(x)\),也就是\(\Gamma(x)\)是唯一满足以上条件的函数。
如下函数被称为Digamma函数,
$$\Psi(x) = \frac{d\log\Gamma(x)}{dx}$$
这也是一个很重要的函数,在涉及求Dirichlet分布相关的参数的极大似然估计时,往往需要使用到这个函数。Digamma函数具有如下一个漂亮的性质
$$ \Psi(x+1) = \Psi(x) + \frac{1}{x} $$
函数\(\Psi(x)\)和欧拉常数\(\gamma\)以及\(\zeta\)函数都有密切关系,令
$$\Psi_n(x) = \frac{d^{n+1}\log\Gamma(x)}{dx^{n+1}}$$
则\(\Psi_0(x) = \Psi(x)\),可以证明
$$\Psi(1) = -\gamma, \Psi(2) = 1-\gamma$$
$$\Psi_1(1) = \zeta(2) = \frac{\pi^2}{6}, \Psi_2(1) = -2\zeta(3)$$
所以Gamma函数在数学上是很有魅力的,它在数学上应用广泛,不仅能够被一个理科本科生很好的理解,本身又足够的深刻,具有很多漂亮的数学性质,历史上吸引了众多一流的数学家对它进行研究。美国数学家Philip J.Davis写了篇很有名的介绍Gamma函数的文章:“Leonhard Euler’s Integral: A Historical Profile of the Gamma Function”,文中对Gamma函数一些特性发现的历史进行了很详细的描述,这篇文章获得了 Chauvenet Prize(美国数学会颁发的数学科普最高奖)。
(本小节主要是数学欣赏,如果对某些概念不熟悉,就略过吧:-))
1.3 从二项分布到Gamma分布
Gamma函数在概率统计中频繁现身,众多的统计分布,包括常见的统计学三大分布(\(t\)分布,\(\chi^2\)分布,\(F\)分布)、Beta分布、Dirichlet 分布的密度公式中都有Gamma函数的身影;当然发生最直接联系的概率分布是直接由Gamma函数变换得到的Gamma分布。对Gamma函数的定义做一个变形,就可以得到如下式子
$$ \int_0^{\infty} \frac{x^{\alpha-1}e^{-x}}{\Gamma(\alpha)}dx = 1 $$
于是,取积分中的函数作为概率密度,就得到一个形式最简单的Gamma 分布的密度函数
$$Gamma(x|\alpha) = \frac{x^{\alpha-1}e^{-x}}{\Gamma(\alpha)} $$
如果做一个变换\(x=\beta t\),就得到Gamma分布的更一般的形式
$$Gamma(t|\alpha, \beta) = \frac{\beta^\alpha t^{\alpha-1}e^{-\beta t}}{\Gamma(\alpha)} $$
其中\(\alpha\)称为shape parameter,主要决定了分布曲线的形状;而\(\beta\)称为rate parameter或者inverse scale parameter(\(\frac{1}{\beta}\)称为scale parameter),主要决定曲线有多陡。
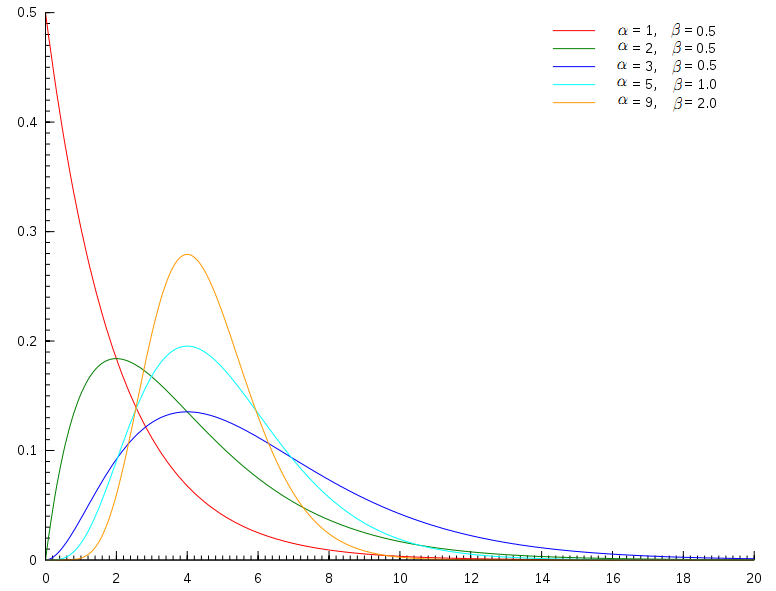
\(Gamma(t|\alpha,\beta)\)分布图像
Gamma分布在概率统计领域也是一个万人迷,众多统计分布和它有密切关系。指数分布和\(\chi^2\)分布都是特殊的Gamma分布。另外Gamma分布作为先验分布是很强大的,在贝叶斯统计分析中被广泛的用作其它分布的先验。如果把统计分布中的共轭关系类比为人类生活中的情侣关系的话,那指数分布、Poission分布、正态分布、对数正态分布都可以是Gamma分布的情人。接下来的内容中中我们主要关注\(\beta = 1\)的简单形式的Gamma分布。
Gamma分布首先和Poisson分布、Poisson过程发生密切的联系。我们容易发现Gamma分布的概率密度和Poisson分布在数学形式上具有高度的一致性。参数为\(\lambda\)的Poisson分布,概率写为
$$Poisson(X=k|\lambda) = \frac{\lambda^k e^{-\lambda}}{k!} $$
在Gamma分布的密度中取\(\alpha = k+1\)得到
$$Gamma(x|\alpha=k+1) = \frac{x^ke^{-x}}{\Gamma(k+1)}= \frac{x^k e^{-x}}{k!} $$
所以这两个分布数学形式上是一致的,只是Poisson分布是离散的,Gamma分布是连续的,可以直观的认为Gamma分布是 Poisson 分布在正实数集上的连续化版本。
这种数学上的一致性是偶然的吗?这个问题我个人曾经思考了很久,终于想明白了从二项分布出发能把Gamma分布和Poisson分布紧密联系起来。我们在概率统计中都学过\(Poisson(\lambda)\)分布可以看成是二项分布\(B(n,p)\)在\(np=\lambda, n \rightarrow \infty\)条件下的极限分布。如果你对二项分布关注的足够多,可能会知道二项分布的随机变量\(X\sim B(n,p)\)满足如下一个很奇妙的恒等式
\begin{equation} \label{binomial-beta} P(X \le k) = \frac{n!}{k!(n-k-1)!} \int_p^1 t^k(1-t)^{n-k-1} dt \quad (*) \end{equation}
这个等式反应的是二项分布和Beta分布之间的关系,证明并不难,它可以用一个物理模型直观的做概率解释,而不需要使用复杂的数学分析的方法做证明。由于这个解释和Beta分布有紧密的联系,所以这个直观的概率解释我们放到下一个章节,讲解Beta/Dirichlet分布的时候进行。此处我们暂时先承认(*)这个等式成立。我们在等式右侧做一个变换\(t=\frac{x}{n}\),得到
\begin{align} P(X \le k) & = \frac{n!}{k!(n-k-1)!} \int_p^1 t^k(1-t)^{n-k-1} dt \notag \\ & = \frac{n!}{k!(n-k-1)!} \int_{np}^{n} (\frac{x}{n})^k(1-\frac{x}{n})^{n-k-1} d\frac{x}{n} \notag \\ & = \frac{(n-1)!}{k!(n-k-1)!} \int_{np}^{n} (\frac{x}{n})^k(1-\frac{x}{n})^{n-k-1} dx \notag \\ & = \int_{np}^{n} \binom{n-1}{k}(\frac{x}{n})^k(1-\frac{x}{n})^{n-k-1} dx \notag \\ & = \int_{np}^{n} Binomial(Y=k|n-1,\frac{x}{n})dx \end{align}
上式左侧是二项分布\(B(n,p)\),而右侧为无穷多个二项分布\(B(n-1,\frac{x}{n})\)的积分和,所以可以写为
\begin{equation} \label{binomial-beta-binomial} Binomial(X \le k|n,p) = \int_{np}^{n} Binomial(Y=k|n-1,\frac{x}{n})dx \quad \end{equation}
实际上,对上式两边在条件\(np=\lambda, n \rightarrow \infty\)下取极限,则左边有\(B(n,p) \rightarrow Poisson(\lambda)\),而右边有\(B(n-1,\frac{x}{n}) \rightarrow Poisson(x)\),所以得到
\begin{equation} Poisson(X \le k|\lambda) = \int_\lambda^\infty Poisson(Y=k|x)dx \end{equation}
把上式右边的Possion分布展开,于是得到
$$ Poisson(X \le k|\lambda) = \int_\lambda^\infty Poisson(Y=k|x)dx = \int_\lambda^\infty \frac{x^k e^{-x}}{k!} dx $$
所以对于们得到如下一个重要而有趣的等式
\begin{equation} \label{poisson-gamma} Poisson(X \le k|\lambda) = \int_\lambda^\infty \frac{x^k e^{-x}}{k!} dx \quad (**) \end{equation}
接下来我们继续玩点好玩的,对上边的等式两边在\(\lambda \rightarrow 0\)下取极限,左侧Poisson分布是要至少发生k个事件的概率,\(\lambda \rightarrow 0\)的时候就不可能有事件发生了,所以\(P(X \le k)\rightarrow 1\),于是我们得到
$$ 1 = \lim_{\lambda \rightarrow 0} \int_\lambda^\infty \frac{x^k e^{-x}}{k!} dx = \int_0^\infty \frac{x^k e^{-x}}{k!} dx $$
在这个积分式子说明\(f(x) = \frac{x^k e^{-x}}{k!}\)在正实数集上是一个概率分布函数,而这个函数恰好就是Gamma分布。我们继续把上式右边中的\(k!\)移到左边,于是得到
$$ k! = \int_0^\infty x^k e^{-x} dx $$
于是我们得到了\(k!\)表示为积分的方法。
看,我们从二项分布的一个等式出发,同时利用二项分布的极限是Possion分布这个性质,基于比较简单的逻辑,推导出了Gamma分布,同时把\(k!\)表达为Gamma函数了!实际上以上推导过程是给出了另外一种相对简单的发现Gamma函数的途径。
回过头我们看看(**)式,非常有意思,它反应了Possion分布和Gamma分布的关系,这个和(*)式中中反应的二项分布和Beta分布的关系具有完全相同的结构。把(**)式变形一下得到
$$ Poisson(X \le k|\lambda) + \int_0^\lambda\frac{x^k e^{-x}}{k!}dx = 1 $$
我们可以看到,Poisson分布的概率累积函数和Gamma分布的概率累积函数有互补的关系。
其实(*)和(**)这两个式子都是陈希儒院士的《概率论与数理统计》这本书第二章的课后习题,不过陈老师习题答案中给的证明思路是纯粹数学分析的证明方法,虽然能证明等式成立,但是看完证明后无法明白这两个等式是如何被发现的。上诉的论述过程说明,从二项分布出发,这两个等式都有可以很好的从概率角度进行理解。希望以上的推导过程能给大家带来一些对Gamma函数和Gamma分布的新的理解,让Gamma分布不再神秘。

发表/查看评论