公元1777年,法国科学家D·布丰(D.Buffon 1707~1788)设计了一个巧夺天工的实验:往间距为a的平行线族之间投掷长为L 的针,可以计算出针和平行线相交的概率为:

根据此式,可以得到pi的近似估计值,这的确是一个伟大的、奇妙而划时代的实验,可算是蒙特卡罗模拟中的鼻祖和经典了。在大多数教材上,这个概率都是用积分或二重积分计算得来的,比较繁琐,在matrix67的博客中,我欣慰而惊奇地看到了一种非常简便、直观的解法,感慨了一番,也稍微思考了一番。
期望值的一个最引人注目的性质就是,E(A+B)=E(A)+E(B),不管A和B是不是独立的。想象一根长度为L的铁丝,不管它被弯成了什么形状,扔到地上后它与地板上的平行线的交点个数的期望值都是一样的,并且这个值是和L成正比的。这是因为,我们可以把一根弯铁丝看作很多很多小的直线段构成;而每个充分小的直线段与平行线交点个数的期望都是相同的,那么由期望值的线性关系,整个弯铁丝与平行线交点数的期望就是c·L,其中c是某个固定的系数。为了求出这个系数是多少,我们只需要考虑一些特殊的情况。注意到,把一根长度为pi的铁丝弯成一个直径为1的圆,则把它扔到地上之后,它与这组平行线总有两个交点。这就是说,pi的c倍就等于2,即c等于2/pi。自然,一根单位长度的针与平行线的交点个数的期望值就是2/pi;而由于这根针与平行线要么没有交点,要么就只有一个交点,因此这个数值就相当于是针与平行线相交的概率了。——matrix67
matrix67是北大中文系的学生,他对数学思维的把握令我十分汗颜。期望的这条性质大家知道,但是离灵活运用却差得很远。根据上述理论,很容易得到,对于任何曲线,它和平行线族交点个数(Y)的期望都是:

其中S是该曲线周长。
如果要向平行线族之间投掷凸n边形(或者扩展到凸域,凸域就是过该图形任一点做切线,那么所有的点都在切线的同侧,也就是没有凹进去的部分),如果这个凸域的直径不大于平行线距离a的话,那么它和平行线族相交的概率为:

其中,S为凸区域的周长。
概率值刚好是交点个数期望的一半,这个也很直观,因为凸域和平行线的交点个数只有三种可能:
- 1个交点:当凸域和平行线相切,或者顶点重合
- 2个交点:这种情况是最常见的
- 无穷多个交点:有一边重合的时候
其中,第一种情况和第三种情况的几何概率为零,故概率值刚好是交点个数期望的一半(这里不太严谨,望大家指教)。把两根针并在一起,既可以构造一个闭区域,其与平行线相交的概率和交点个数都和上面理论一致。
如果投掷一般闭合区域的话,那么它和平行线族相交的概率依然为:

不过,此时S为该闭区域所生成的最小凸区域的周长。
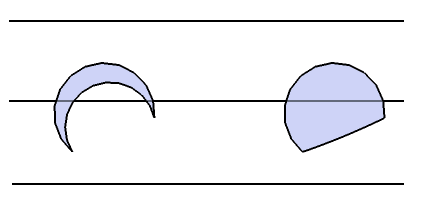
因为尽管它们的周长不一样,和平行线交点的期望不一样,但是它们和平行线是否有交点的概率是一样的。下图中的类半圆图形就是月牙图形生成的最小凸区域,它们显然和平行线是否相交完全等价。
最后,要说的是直观思维的重要性,定理有千千万万,如果能用直观的形式将它们逐渐消化,那是最好不过的了,我在看书的时候经常能把一个定理啃下来,但是还是觉得对这个定理依然云里雾里的。对此,matrix67做了很精彩的评价:
数学学习真正悲哀的就是,记住了某个神奇而伟大的定理,看懂了其最严密的推导过程,但却始终没能直观地去理解它。虽然严密的推导是必要的,直观理解往往是不准确的,但如果能悟出一个让定理一瞬间变得很显然的解释,这不但是一件很酷的事,而且对定理更透彻的理解和更熟练的运用也很有帮助。

发表/查看评论