多元数据的可视化方法很多,譬如散点图、星图、雷达图、脸谱图、协同图等,大致可分为以下几类:1.基于点(如二维、三维散点图);2.基于线(如轮廓图、调和曲线图);3.基于平面图形(如星图、雷达图、蛛网图);4.基于三维曲面(如三维曲面图)。其思想是将高维数据映射到低维空间(三维以下)内,尽量使信息损失最少,同时又能利于肉眼辨识。调和曲线图和轮廓图(即平行坐标图)都是多元数据的可视化方法,它们基于“线”的形式,将多元数据表示出来,对于聚类分析有很好的帮助。
轮廓图
轮廓图的思想非常简单、直观,它是在横坐标上取 p 个点,依次表示各个指标(即变量);横坐标上则对应各个指标的值(或者经过标准化变换后的值),然后将每一组数据对应的点依次连接即可。
lattice 包中的 parallel() 函数可以轻松绘出轮廓图。利用 iris 数据,以下代码可以画出其轮廓图(图1)。
library(lattice)
data(iris)
parallel(~iris[1:4], iris, groups = Species,
horizontal.axis = FALSE, scales = list(x = list(rot = 90)))
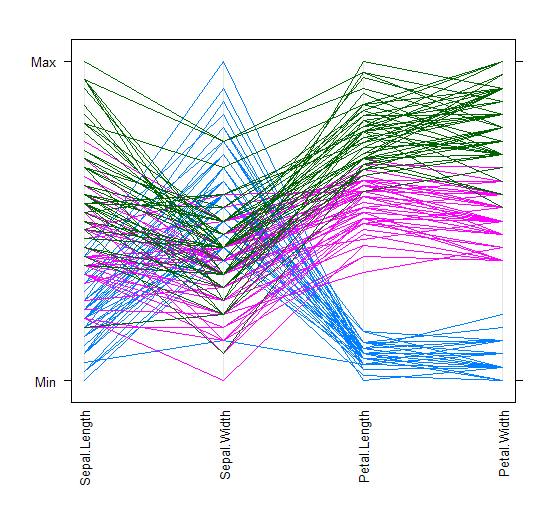
图1 Iris 数据的轮廓图(Parallel Coordinate Plots)
观察图1,可以发现同一品种的鸢尾花的轮廓图粗略地聚集在一起。
调和曲线图
调和曲线图的思想和傅立叶变换十分相似,是根据三角变换方法将 p 维空间的点映射到二维平面上的曲线上。假设 $X_r$ 是 p 维数据的第 r 个观测值,即
$$X_r^T=(x_{r1}, \cdots , x_{rp})$$
则对应的调和曲线是
$$f_r(t)=\frac{x_{r1}}{\sqrt{2}} +x_{r2}\sin t+x_{r3} \cos t+x_{r4}\sin2 t+x_{r5} \cos2 t+\cdots$$
其中$-\pi \leq t \leq \pi$.
同样利用 iris 数据,下面代码(主要取自《统计建模与R软件》,尚未优化)可以画出其调和曲线图(图2)。
x = as.matrix(iris[1:4])
t = seq(-pi, pi, pi/30)
m = nrow(x)
n = ncol(x)
f = matrix(0, m, length(t))
for (i in 1:m) {
f[i, ] = x[i, 1]/sqrt(2)
for (j in 2:n) {
if (j%%2 == 0)
f[i, ] = f[i, ] + x[i, j] * sin(j/2 * t)
else f[i, ] = f[i, ] + x[i, j] * cos(j%/%2 * t)
}
}
plot(c(-pi, pi), c(min(f), max(f)), type = "n", main = "The Unison graph of Iris",
xlab = "t", ylab = "f(t)")
for (i in 1:m) lines(t, f[i, ], col = c("red", "green3",
"blue")[unclass(iris$Species[i])])
legend(x = -3, y = 15, c("setosa", "versicolor", "virginica"),
lty = 1, col = c("red", "green3", "blue"))
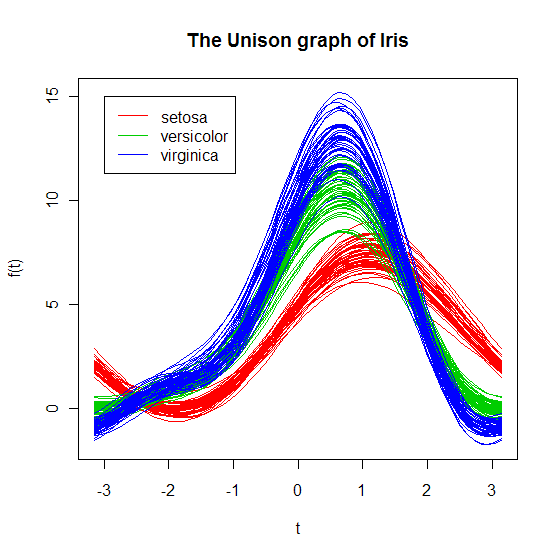
图2 Iris 数据的调和曲线图
观察图2,同样可以发现同一品种鸢尾花数据的调和曲线图基本上扭在一起。同图1 比较后,发现图2 更加清楚明白,事实上Andrews证明了调和曲线图有许多良好性质。
讨论
轮廓图和调和曲线图有着相近的功能,而技巧大有不同。轮廓图简单却现得粗糙,调和曲线图公式复杂却十分精细。从这一个侧面可以发现直观的统计思想固然重要,但存在很多种不可能通过直观思想得到的、而又非常精细、美妙的方法,此时倍受众多统计学家责难的数学显得优雅而又强大。

发表/查看评论